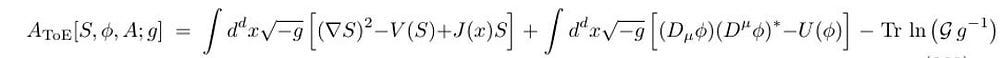The Obidi Action and the Mathematical Rigour of the Theory of Entropicity (ToE): Beauty and Truth in the Equations of Nature and Reality

 The Obidi Action and the Mathematical Rigour of the Theory of Entropicity (ToE)

Beauty and Truth in the Equations of Nature and Reality

The equations of the Theory of Entropicity (ToE) are designed with a high degree of mathematical rigor, though some components are still undergoing formalization and peer review.

Prologue

“…Einstein’s field equations are so beautiful that they must be true…” ~Lev Davidovich Landau

Below is the gauge sectored form of the Obidi Action of the Theory of Entropicity (ToE)

The Obidi Action of the Theory of Entropicity (ToE)

The Obidi Action of the Theory of Entropicity (ToE)

Here’s a breakdown of the current state of rigor and structure of the mathematical formulation of the Theory of Entropicity (ToE):

🧮 Core Mathematical Framework

• Obidi Action & Master Entropic Equation (MEE): These form the backbone of ToE’s field-theoretic formulation. The Obidi Action is a variational principle from which the MEE is derived, analogous to how the Einstein-Hilbert action yields Einstein’s field equations.

• Entropic Geodesics & Entropy Potential Equation: These equations govern the motion of systems in entropic spacetime, replacing geodesics in curved spacetime with entropy-gradient-driven trajectories.

• Information Geometry Integration: ToE incorporates the Fisher–Rao and Fubini–Study metrics via the Amari–Čencov α-connection, grounding its dynamics in a rigorous information-geometric framework.

🧠 Novel Constructs with Formal Definitions

• Self-Referential Entropy (SRE) Formalism: Introduces the SRE Index and Clone Theorems, which quantify internal entropic feedback and constraints on information duplication at both quantum and macroscopic levels.

• Entropic CPT Symmetry & Noether Principle: These extend classical symmetry principles to entropic fields, yielding new conservation laws and a thermodynamic uncertainty relation.

• Entropion Field Quanta: The theory posits quantized excitations of the entropic field — “entropions” — with dynamics governed by the MEE, though their full quantum field treatment is still under development.

🔍 Current Limitations and Ongoing Formalization

• While the conceptual architecture is robust, some equations — especially those involving context-dependent entropic thresholds and entropy-driven decoherence rates — are still being refined for mathematical completeness and testability.

• The theory’s non-reliance on spacetime curvature and its replacement of gravitational geometry with entropy gradients is a radical departure from General Relativity, and although it reproduces key results (e.g. Mercury’s perihelion precession), it demands new mathematical tools for full validation.

🧭 Summary

The Equations of the Theory of Entropicity (ToE) are rigorous in intent and structure, grounded in variational principles, information geometry, and symmetry analysis. However, some components remain in pre-peer-review stages, and experimental testability and formal closure are active areas of development

References

Further Resources on the Theory of Entropicity (ToE):

1. Website: Theory of Entropicity ToE — https://theoryofentropicity.blogspot.com

2. LinkedIn: Theory of Entropicity ToE — https://www.linkedin.com/company/theory-of-entropicity-toe/about/?viewAsMember=true

3. Substack: Theory of Entropicity (ToE) — John Onimisi Obidi | Substack

4. Medium: Theory of Entropicity (ToE) — John Onimisi Obidi — Medium

5. SciProfiles: Theory of Entropicity (ToE) — John Onimisi Obidi | Author

6. Encyclopedia.pub: Theory of Entropicity (ToE) — John Onimisi Obidi | Author

7. HandWiki contributors, “Biography: John Onimisi Obidi,” HandWiki, https://handwiki.org/wiki/index.php?title=Biography:John_Onimisi_Obidi&oldid=2743427 (accessed October 31, 2025).

8. HandWiki Contributions: Theory of Entropicity (ToE) — John Onimisi Obidi | HandWiki

9. HandWiki Home: Theory of Entropicity (ToE) — John Onimisi Obidi | HandWiki

10. HandWiki Homepage-User Page: Theory of Entropicity (ToE) — John Onimisi Obidi | HandWiki

11. Academia: Theory of Entropicity (ToE) — John Onimisi Obidi | Academia

12. ResearchGate: Theory of Entropicity (ToE) — John Onimisi Obidi | ResearchGate

13. Figshare: Theory of Entropicity (ToE) — John Onimisi Obidi | Figshare

14. Authoria: Theory of Entropicity (ToE) — John Onimisi Obidi | Authorea

15. Social Science Research Network (SSRN): Theory of Entropicity (ToE) — John Onimisi Obidi | SSRN

16. 15. Wikidata contributors, Biography: John Onimisi Obidi “Q136673971,” Wikidata, https://www.wikidata.org/w/index.php?title=Q136673971&oldid=2423782576 (accessed October 31, 2025).

17. 16. Google Scholar: ‪John Onimisi Obidi — ‪Google Scholar

18. 17. Cambridge University Open Engage (CoE): Collected Papers on the Theory of Entropicity (ToE)

Analysis of John Onimisi Obidi’s Theory of Entropicity (ToE) and David Sigtermans Total Entropic Quantity (TEQ): Converging Paths Toward the Foundations of Nature and Reality

Analysis of John Onimisi Obidi’s Theory of Entropicity (ToE) and David Sigtermans Total Entropic Quantity (TEQ)

Converging Paths Toward the Foundations of Nature and Reality

Introduction: Entropy‑Based Frameworks in Physics

The quest to understand the foundations of nature and reality has led to two groundbreaking entropy‑driven frameworks: David Sigtermans’ Theory of Total Entropic Quantity (TEQ) and John Onimisi Obidi’s Theory of Entropicity (ToE). While TEQ explains how physical structure emerges from curved entropy geometry, ToE advances this vision by treating entropy itself as the fundamental dynamical field that drives spacetime, matter, and information.

In this comparative overview, we explore how ToE functions as a superset of TEQ, absorbing TEQ’s core constructs — such as entropy curvature, resolution boundaries, and entropy‑weighted dynamics — into a broader entropic manifold governed by variational principles, unified metrics, and deformation parameters. By situating TEQ within its entropic Noether framework and extending entropy‑driven conservation laws, ToE not only recovers standard physics in limiting cases but also provides a meta‑theoretical foundation for unifying gravity, quantum mechanics, and information theory.

This relationship highlights the growing importance of entropy‑based cosmology and information geometry in modern theoretical physics, offering a pathway toward a deeper understanding of reality’s underlying structure.

Overview of ToE and TEQ relationship

TEQ treats physical structure as emergent from curved entropy geometry; ToE treats entropy itself as the fundamental dynamical field driving reality. In that sense, ToE generalizes TEQ’s ontology and methods, absorbing TEQ’s “entropy curvature,” “resolution boundaries,” and “entropy-weighted dynamics” as special cases within a broader entropic manifold governed by variational principles, unified metrics, and deformation parameters. ToE recovers standard physics in limits, while keeping TEQ-like constructs as localized models of entropic dynamics. Moreover, ToE explicitly analyzes and extends TEQ in its own corpus, situating TEQ inside an entropic Noether framework and entropy-driven conservation.

Core Axioms and Constructs Comparison Between ToE and TEQ

How ToE Becomes a Superset Mathematically

Entropy field and curvature

• Field elevation: ToE promotes entropy to a continuous dynamical field whose gradients generate motion, gravitation, time, and information flow. TEQ’s “curved entropy geometry” is naturally interpreted as the geometry induced by this field; TEQ’s curvature is a subset of ToE’s entropic manifold constructions.

Unified metric structure and “resolution boundaries”

• Metric fusion: ToE unifies Fisher–Rao (classical) and Fubini–Study (quantum) metrics through the Amari–Čencov α‑connection. TEQ’s “resolution boundaries” map to finite‑information/finite‑resolution slices in this metric family; the α parameter acts as a deformation index controlling coarse‑to‑fine entropic resolution and curvature strength, embedding TEQ’s boundary logic as one regime of ToE’s metric geometry.

Entropy‑weighted dynamics and path integrals

• Variational and integral forms: ToE’s Obidi Action yields entropic geodesics and a master evolution equation; its Vuli‑Ndlela Integral is an entropy‑weighted reformulation of Feynman’s path integral that introduces irreversibility. TEQ’s “entropy‑weighted dynamics” and path‑integral derivations appear as special cases where the weight functional and boundary conditions match ToE’s integrals under appropriate α and potential choices.

Stable distinction and causality tensors

• Causal structure: TEQ’s stable distinction pairs with ToE’s causal substrate: entropy gradients define causal arrows and irreversibility. ToE’s entropic Noether perspective links conservation laws to entropy‑constrained symmetries, generalizing TEQ’s information‑theoretic causal tensors within a broader conservation framework.

Scope and limits: why TEQ sits inside ToE

• Limiting recoveries: ToE reproduces Einstein’s field equations as a limit and subsumes entropy‑gravity approaches, which means TEQ’s gravitational and thermodynamic constructs can be recovered within ToE’s parameter regimes and boundary conditions. This positions TEQ as a domain‑specific instantiation of ToE’s general entropic dynamics.
• Meta‑theory stance: Public comparative treatments have explicitly concluded ToE functions as a broader meta‑framework under which applied entropy models like TEQ can be contextualized, reinforcing the superset claim in both conceptual and mathematical terms.

Practical Mapping from TEQ to ToE

• TEQ entropy curvature → ToE entropic manifold curvature: match via α‑connection choice and entropy potential.
• TEQ resolution boundaries → ToE finite‑information slices: set α and metric scales to encode boundary‑dependent dynamics.
• TEQ entropy‑weighted dynamics → ToE Vuli‑Ndlela Integral: choose weighting functional consistent with TEQ’s axioms; irreversibility emerges naturally.
• TEQ causal tensors → ToE entropic Noether symmetries: derive conservation relations from entropy‑constrained invariances, extending TEQ’s inference tools.

The Overarching Scope of the Theory of Entropicity (ToE)

The Theory of Entropicity is a superset of Total Entropic Quantity because it elevates entropy to a fundamental field with a unified geometric and variational structure, provides entropy‑weighted quantum dynamics with irreversibility, and recovers standard physics in limits; TEQ’s constructs — entropy curvature, resolution boundaries, and entropy‑weighted dynamics — arise as special regimes within ToE’s entropic manifold and action principles, a relationship explicitly analyzed and extended in ToE’s published work.

References

Further Resources on the Theory of Entropicity (ToE):

1. Website: Theory of Entropicity ToE - https://theoryofentropicity.blogspot.com

2. LinkedIn: Theory of Entropicity ToE - https://www.linkedin.com/company/theory-of-entropicity-toe/about/?viewAsMember=true

3. Substack: Theory of Entropicity (ToE) - John Onimisi Obidi | Substack

4. Medium: Theory of Entropicity (ToE) - John Onimisi Obidi – Medium

5. SciProfiles: Theory of Entropicity (ToE) - John Onimisi Obidi | Author

6. Encyclopedia.pub: Theory of Entropicity (ToE) - John Onimisi Obidi | Author

7. HandWiki contributors, “Biography: John Onimisi Obidi,” HandWiki, https://handwiki.org/wiki/index.php?title=Biography:John_Onimisi_Obidi&oldid=2743427 (accessed October 31, 2025).

8. HandWiki Contributions: Theory of Entropicity (ToE) - John Onimisi Obidi | HandWiki

9. HandWiki Home: Theory of Entropicity (ToE) - John Onimisi Obidi | HandWiki

10. Academia: Theory of Entropicity (ToE) - John Onimisi Obidi | Academia

11. ResearchGate: Theory of Entropicity (ToE) - John Onimisi Obidi | ResearchGate

12. Figshare: Theory of Entropicity (ToE) - John Onimisi Obidi | Figshare

13. Authoria: Theory of Entropicity (ToE) - John Onimisi Obidi | Authorea

14. Social Science Research Network (SSRN): Theory of Entropicity (ToE) - John Onimisi Obidi | SSRN

15. Wikidata contributors, Biography: John Onimisi Obidi “Q136673971,” Wikidata, https://www.wikidata.org/w/index.php?title=Q136673971&oldid=2423782576 (accessed October 31, 2025).

16. Google Scholar: ‪John Onimisi Obidi — ‪Google Scholar

17. Cambridge University Open Engage (CoE): Collected Papers on the Theory of Entropicity (ToE)

Suggested Reading

[1] Obidi, John Onimisi (2025). On the Conceptual and Mathematical Foundations of the Theory of Entropicity (ToE): An Alternative Path toward Quantum Gravity and the Unification of Physics.

[2] Physics:HandWiki Master Index of Source Papers on Theory of Entropicity(ToE). (2025, September 9). HandWiki. Retrieved 17:33, September 9, 2025

[3] Obidi, John Onimisi. Conceptual and Mathematical Foundations of Theory of Entropicity(ToE). Encyclopedia. Available online.

[4] Wissner-Gross, A. D., & Freer, C. E. (2013). Causal Entropic Forces. Physical Review Letters.

[5] Amari, S. (2016). Information Geometry and Its Applications. Springer.

[6] Jaynes, E. T. (1957). Information Theory and Statistical Mechanics. Physical Review.

[7] Nielsen, M. A., & Chuang, I. L. (2010). Quantum Computation and Quantum Information. Cambridge University Press.

[8] Vidal, G. (2008). Class of Quantum Many-Body States That Can Be Efficiently Simulated. Physical Review Letters.

[9] Methods of Information Geometry — Shun-ichi Amari & Hiroshi Nagaoka (American Mathematical Society, 2000)

[10] The Vuli-Ndlela Integral in the Theory of Entropicity (ToE) — John Onimisi Obidi (2025)

[11] The Obidi Action and the Foundation of the Entropy Field Equation — John Onimisi Obidi (2025)

[12] The Master Entropic Equation (MEE) — John Onimisi Obidi (2025)

[13] Psych entropy and the Entropy of the Mind — John Onimisi Obidi (2025)

[14] Bianconi, G. (2009). Entropy of network ensembles. Physical Review E.

[15] Bianconi, G., & Barabási, A.-L. (2001). Competition and multiscaling in evolving networks. Europhysics Letters.

[16] Ginestra Bianconi. Gravity from entropy. Phys Rev D. 2025 Mar 3;111(6):066001.